Tuning magnetic and valence-bond-solid (VBS) order in the cuprate superconductors

Given the picture of competing orders and quantum phase transitions in the cuprate superconductors (reviewed in S. Sachdev, Science 288, 475 (2000); cond-mat/0009456), it is natural to search for an external parameter which will tune systems across such transitions. An attractive candidate is the magnitude of an applied magnetic field. In strongly type-II superconductors like the cuprates, above a small lower critical field, a magnetic field perpendicular to the layers induces a triangular lattice of vortices: superconductivity is completely suppressed in the very small vortex cores, and these are surrounded by regions of superflow of Cooper pairs (see Figure 3 below).

The cores of these vortices are one place that might carry a competing order. This was suggested in S. Sachdev, Physical Review B 45, 389 (1992) (and also by N. Nagaosa and P. A. Lee, Physical Review B 45, 966 (1992)), where the vortex core contained enhanced dynamic antiferromagnetic correlations , i.e. a quantum paramagnet with a spin gap. Initially, in the simplest mean field theory, these enhanced dynamic spin correlations appeared only in vortices with magnetic flux hc/e, but more involved mean-field theories showed these could also appear in vortices with magnetic flux hc/2e (see reviews in X.-G. Wen and P. A. Lee, Physical Review Letters 76, 503 (1996), P. A. Lee and X.-G. Wen", Physical Review B 63, 224517 (2001)). S.-C. Zhang, Science 275, 1089 (1997) and D. Arovas et al., Physical Review Letters 79, 2871 (1997), described discussed nucleation of static Neel order in the vortex core; however, given the small size of the cores, we expect that dynamic quantum spin fluctuations would disrupt the Neel order, and restore spin gap behavior. Studies discussed in the pages on insulating antiferromagnets, magnetic quantum criticality and valence-bond-solid (VBS) order in doped antiferromagnets suggested that a fundamental characteristic of the spin gap behavior in doped antiferromagnets is the breaking of translational symmetry by the appearance of VBS order. This reasoning led to the first prediction, by K. Park and S. Sachdev, Physical Review B 64, 184510 (2001), of VBS order near the vortex cores in a superconductor with dynamically fluctuating spins which preserve spin rotation invariance (more on the results of this paper below).

Further theoretical progress was stimulated by neutron scattering experiments (B. Lake et al., Science 291, 1759 (2001)) which observed an enhancement of low energy, dynamic spin fluctuations in the presence of an applied magnetic field. These spin density wave (SDW) fluctuations were at a wavevector K=2p(1/2-e,1/2), where e >0 varied as a function of carrier concentration; the Neel state has e=0. It was argued in paper 1 (papers are listed at the bottom of this page) that the proper way to address the theoretical questions, and to describe the experiments, is to follow the field dependence of the magnetic quantum critical point between the states with and without long-range spin density wave (SDW) order, in a background superconducting (SC) state (i.e. the critical point between the SC+SDW and SC states). This analysis immediately showed that the dominant influence of the magnetic field arises not in the vortex cores, but from the much larger regions of superflow around the vortices: it is the superflow which influences the competition between orders, and enhances the low energy spin fluctuations.

The main predictions of paper 1 (presented in considerable detail in paper 4) are the phase diagram in Figure 1, and the physical properties of the lower field phases.


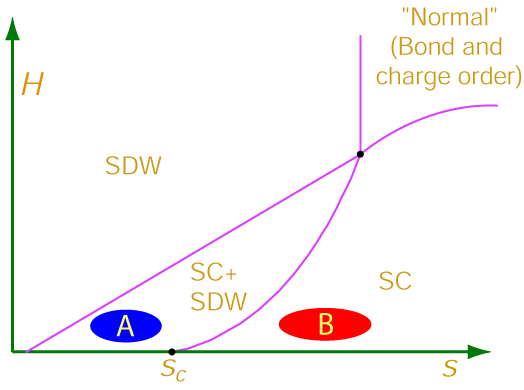
Figure 1. Influence of a magnetic field on a transition between a superconductor with co-existing spin density wave order (SC+SDW state) and an ordinary superconductor (the SC state). The spin density wave is dynamically fluctuating the SC phase, but is static in the SC+SDW phase. The zero-field transition as a function of s is the same as that as a function of g discussed in the category of magnetic quantum criticality, and s increases as a function of carrier concentration. The theory predicts that the phase boundary between these phases has a critical H which decreases as (s-sc)/(ln(1/(s-sc))). Experimental test of our predictions have so far been carried out in regions A and B.

The experiments of B. Lake et al., Science 291, 1759 (2001), are in region B of Figure 1, in the SC phase. Because the phase boundary to SC+SDW order comes in with vanishing slope, a moderate field is sufficient to drive the system quite close to the transition to the SC+SDW phase: this is our explanation for the observed enhancement of low energy spin fluctuations.

A different set of experiments have been carried out in region A of Figure 1: here there is long-range spin density wave order which is enhanced and modulated by the magnetic field, as illustrated Figures 2 and 3.


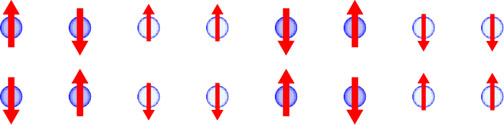
Figure 2. Microscopic structure of the spin density wave on the Cu sites of the high temperature superconductor as deduced from neutron scattering experiments. At finite doping, the ordering wavevector moves away from (p,p ), and shown is a spin density wave at wavevector (3p /4, p ) with a period of 8 lattice spacings in the horizontal direction. The spins are collinearly polarized, and this implies that there is a charge density wave at twice this wavevector (J. Zaanen and O. Gunnarsson, Phys. Rev. B 40, 7391 (1989); H. Schulz, J. de Physique 50, 2833 (1989); O. Zachar, S. A. Kivelson, and V. J. Emery, Phys. Rev. B 57, 1422 (1998)), which is (p /2,0), modulo reciprocal lattice vectors. We believe that the modulation of the site charge density is likely to be negligibly small, and the dominant `charge' order modulation is in spin singlet bond variables like the exchange energy between nearest neighbor sites --- hence the term "VBS order". The period of the VBS order modulation is the same as that of the charge density modulation.

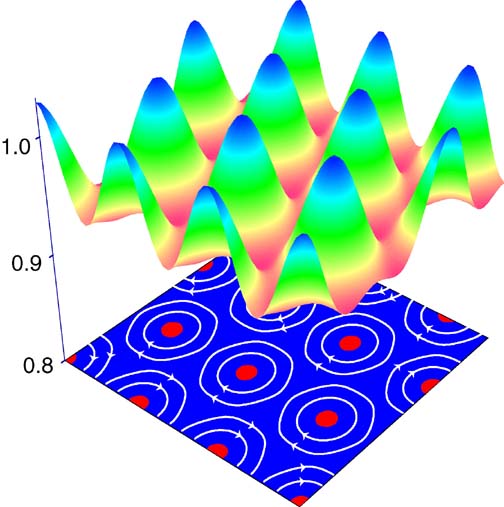
Figure 3. Modulation of an ordered spin-density wave state by a magnetic field in region A of Figure 1 (computations from paper 4). The colored surface is the envelope of the microscopic order shown in Figure 2. The red circles are the vortex cores surrounding which are supercurrents of Cooper pairs. The spacing between vortex cores is on the order of 50-100 Cu lattice spacings.

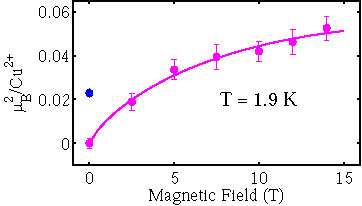
The enhancement of the average amplitude of the spin density wave by a magnetic field has been measured in two neutron scattering experiments (B. Khaykovich et al., Phys. Rev. B 66, 014528 (2002) and B. Lake et al., Nature 415, 299 (2002)), and the results are in good agreement with our predictions, as shown in Figure 4.

Figure 4. Enhancement of the Bragg elastic scattering peak of the spin density wave as a function of magnetic field in region A of Figure 1. The dots are neutron scattering measurements of B. Lake et al., Nature 415, 299 (2002), and the line is the functional form predicted prior to the experiments in paper 1.

The modulation of the colored surface in Figure 3 also implies that there should be satellite Bragg peaks associated with the vortex lattice; however, our computations in paper 4 indicate that these are too weak to be observable in current elastic neutron scattering experiments.

It was predicted in K. Park and S. Sachdev, Physical Review B 64, 184510 (2001) (see the discussion in the second-to-last paragraph on page 184510-12), and in paper 2 below, that the VBS order induced by a magnetic field should be observable in scanning tunnelling microscopy (STM) measurements in the spin gap region B of Figure 1. Note that this is a prediction of static VBS order (and weak associated charge density modulations that are allowed by symmetry) in a region with dynamically fluctuating spin order; so the spins in Figure 2 are rotating rapidly leaving no average magnetic moment, while the VBS order in Figure 2 (represented by the density of the blue color) remains static. These papers also made a connection to our earlier large N studies of superconductors with preserved spin rotation invariance (M. Vojta and S. Sachdev, Physical Review Letters 83, 3916 (1999); M. Vojta, Y. Zhang, and S. Sachdev, Physical Review B 62, 6721 (2000)), whose results are described in the page on translational symmetry breaking in d-wave superconductors (see especially Figure 2 on the linked page): a large doping range had VBS order with a period of four lattice spacings. In the presence of a vortex lattice in the SC phase, the induced static VBS order in the SC phase is inhomogeneous, and the spatial envelope of the VBS order was computed in papers 3 and 4 (for the same set of parameters used to obtain agreement with neutron scattering results); typical results are shown in Figure 5.


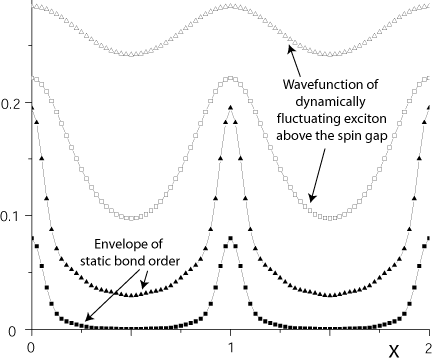
Figure 5. Characteristics of the spin density wave state in region B of Figure 1 at two different magnetic fields (squares and triangles; the squares have the lower field). The orientation of the spins fluctuates with a frequency of order the inverse spin gap; the lowest energy exciton has the wavefunction as shown (open symbols), and this is the envelope of the microscopic order in Figure 2. The presence of the vortex cores (at locations x=0,1,2) pins static VBS order with amplitude as shown (full symbols). Notice that while the dynamic spin correlations are extended across the entire system, the static VBS order is localized relatively close to the vortex cores. The computations are from paper 4.

The disparate length and energy scales controlling spin correlations (as measured in neutron scattering) and VBS order (as measured in STM) arise for the same set of coupling constants and constitute a significant consequence of our theory. Stimulated by our predictions, in K. Park and S. Sachdev, Physical Review B 64, 184510 (2001) and papers 1 and 2, that dominant competition between magnetism and superconductivity takes place in the superflow region outside the core, the group of Seamus Davis at Berkeley undertook STM measurements to detect signatures of VBS order in this region. Their results have been reported recently by Hoffman et al., Science 295, 466 (2002) and are shown in Figure 6; the spatial extent of the observed modulation is in good accord with our computations for the VBS order in Figure 5.

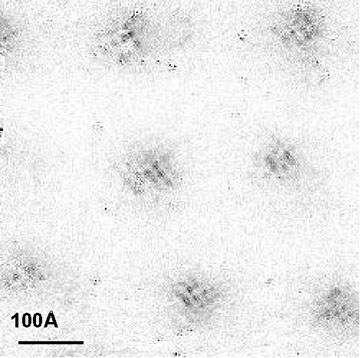
Figure 6. STM measurements of Hoffman et al., Science, 295, 466 (2002) of modulations in the local density of states in region B of Figure 1. The banded structure near each vortex core has a period of four lattice spacings: we interpret it as a signal of the VBS order in Figure 2 . Our theoretical prediction for the envelope of this VBS order is shown in Figure 5, and its spatial extent is in good accord with the measurements above.
See also the article by Barbara Levi in Physics Today, volume 55, number 2, page 14 (2002).

PAPERS

  1. Spin ordering quantum transitions of superconductors in a magnetic field, E. Demler, S. Sachdev and Y. Zhang, Physical Review Letters 87, 067202 (2001); cond-mat/0103192.
  2. Spin and charge order in Mott insulators and d-wave superconductors, S. Sachdev, Proceedings of Spectroscopies of Novel Superconductors, Chicago, May 13-17, 2001, Journal of Physics and Chemistry of Solids 63, 2269 (2002); cond-mat/0108238.
  3. Magnetic field tuning of charge and spin order in the cuprate superconductors, A. Polkovnikov, S. Sachdev, M. Vojta, and E. Demler, Proceedings of Physical Phenomena at High Magnetic Fields-IV, Santa Fe, October 19-25, 2001, G. Boebinger, Z. Fisk, L.P. Gor'kov, A. Lacerda, and J.R. Schieffer eds, World Scientific, Singapore (2002), International Journal of Modern Physics B 16, 3156 (2002); cond-mat/0110329.
  4. Competing orders in a magnetic field: spin and charge order in the cuprate superconductors, Y. Zhang, E. Demler and S. Sachdev, Physical Review B 66, 094501 (2002); cond-mat/0112343.
  5. Tuning order in cuprate superconductors, S. Sachdev and S.-C. Zhang, Science 295, 452 (2002); cond-mat/0201401.
  6. Spin and charge order in the vortex lattice of the cuprates: experiment and theory, S. Sachdev, Developments in Mathematical and Experimental Physics, Volume B: Statistical Physics and Beyond, A. Macias, F. Uribe, and E. Diaz eds, Kluwer Academic, New York (2002); cond-mat/0203363.
  7. Pinning of dynamic spin density wave fluctuations in the cuprate superconductors, A. Polkovnikov, M. Vojta, and S. Sachdev, Physical Review B 65, 220509 (2002); cond-mat/0203176.
  8. Spin collective mode and quasiparticle contributions to STM spectra of d-wave superconductors with pinning, A. Polkovnikov, S. Sachdev, and M. Vojta, Physica C 388-389, 19 (2003) (Erratum: 391, 381 (2003)), Proceedings of the 23rd International Conference on Low Temperature Physics, August 20-27, 2002, Hiroshima, Japan; cond-mat/0208334.
  9. Order and quantum phase transitions in the cuprate superconductors, S. Sachdev, Reviews of Modern Physics 75, 913 (2003); cond-mat/0211005.
  10. Order and quantum phase transitions in the cuprate superconductors (summary), S. Sachdev, Solid State Communications 127, 169 (2003), Proceedings of the Euroconference on Quantum Phases at the Nanoscale, Erice, Italy, 15-20 July 2002.
  11. Competing orders in thermally fluctuating superconductors in two dimensions, S. Sachdev and E. Demler, Physical Review B 69, 144504 (2004); cond-mat/0308024.
  12. Putting competing orders in their place near the Mott transition, L. Balents, L. Bartosch, A. Burkov, S. Sachdev, and K. Sengupta, Physical Review B 71, 144508 (2005); cond-mat/0408329.
  13. Putting competing orders in their place near the Mott transition II: the doped quantum dimer model, L. Balents, L. Bartosch, A. Burkov, S. Sachdev, and K. Sengupta, Physical Review B 71, 144509 (2005); cond-mat/0409470.
  14. Estimating the mass of vortices in the cuprate superconductors, L. Bartosch, L. Balents, and S. Sachdev, cond-mat/0502002.
  15. Competing Orders and non-Landau-Ginzburg-Wilson Criticality in (Bose) Mott transitions , L. Balents, L. Bartosch, A. Burkov, S. Sachdev, and K. Sengupta, Proceedings of ``Physics of Strongly Correlated Electron Systems'', YKIS2004 workshop, Yukawa Institute, Kyoto, Japan, November 2004, Progress of Theoretical Physics Supplement 160, 314 (2005); cond-mat/0504692.
  16. Detecting the quantum zero-point motion of vortices in the cuprate superconductors, L. Bartosch, L. Balents, and S. Sachdev, cond-mat/0602429.
  17. Competition between spin density wave order and superconductivity in the underdoped cuprates, E. G. Moon and S. Sachdev, Physical Review B 80, 035117 (2009); arXiv:0905.2608.
  18. Where is the quantum critical point in the cuprate superconductors ?, S. Sachdev, Talk at the Conference on Quantum Criticality and Novel Phases, Dresden, August 2-5, 2009, Physica Status Solidi B 247, 537 (2010); arXiv:0907.0008.
  19. Quantum criticality and the phase diagram of the cuprates, S. Sachdev, Physica C 470, S4 (2010); Keynote talk, 9th International Conference on Materials and Mechanisms of Superconductivity, Tokyo, Sep 7-12, 2009, arXiv:0910.0846.
  20. Quantum critical point shifts under superconductivity: the pnictides and the cuprates , E. G. Moon and S. Sachdev, Physical Review B 82, 104516 (2010); arXiv:1005.3312.
  21. Topological Defects Coupling Smectic Modulations to Intra-unit-cell Nematicity in Cuprates, A. Mesaros, K. Fujita, H. Eisaki, S. Uchida, J. C. Davis, S. Sachdev, J. Zaanen, M. J. Lawler, and Eun-Ah Kim, Science 333, 426 (2011); arXiv:1108.0487.
  22. Nematicity in the vortex lattice of FeSe, D. Chowdhury, E. Berg, and S. Sachdev, Physical Review B 84, 205113 (2011); arXiv:1109.2600
  23. Competition between superconductivity and nematic order : anisotropy of superconducting coherence length, E. G. Moon and S. Sachdev, Physical Review B 85, 184511 (2012); arXiv:1112.3973.
NEXT ; PREVIOUS ; CATEGORIES