Confining paramagnets and Neel and bond order in two-dimensional antiferromagnets

Confining paramagnets and Neel and valence-bond-solid (VBS) order in two-dimensional antiferromagnets

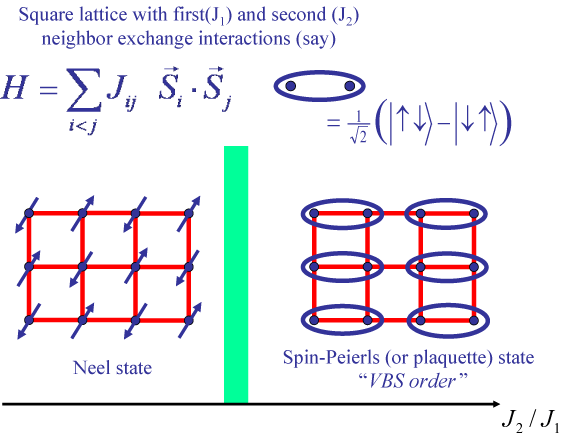
The S=1/2 antiferromagnet on the square lattice is known to have a ground state with Neel long-range order, in which the average spin moments are collinearly polarized in a staggered checkerboard pattern. Suppose we now add frustrating second or further neighbor interactions which destroy the magnetic order in a continuous quantum phase transition, and produce a spin singlet ground state in which average moment on each site is zero. What is the nature of such a ground state ? The following papers argue that, on rather general grounds, destroying collinearly polarized magnetic order leads to a paramagnetic ground state with the following properties :

Broken translational symmetry due to the appearance of valence-bond-solid (VBS) order with at least a four-fold degenerate ground state. A simple possibility is that the ground state is a columnar spin-Peierls state: this state is preferred because it maximizes the "resonance" between nearest neighbor singlet pairings around a plaquette.

Excited states with non-zero spin are created by breaking a singlet bond between a pair of spins. The two S=1/2 moments at the ends of this broken bond ("spinons") are unable to move away from each other (the spinons are confined), and so the lowest excitation is a stable S=1 particle. This particle will appear as a sharp resonance in the neutron scattering cross-section, above a finite energy gap at the magnetic ordering wavevector. We have argued that this resonance is related to observations on the high temperature superconductors.

A great deal of numerical work has been done on the above questions, and two recent references are M.S.L. du Croo de Jongh et al, Physical Review B 62, 14844 (2000), and O.P. Sushkov et al, Physical Review B 63, 104420 (2001).

An experimental study of a pressure-tuned phase diagram of insulating (TMTTF)₂PF₆ by D.S. Chow et al, Physical Review Letters 81, 3984 (1999), yielded results very similar to the theoretical phase diagram above with Neel and spin-Peierls order. Experimental evidence for VBS order in doped antiferromagnets is discussed in a separate category.

PAPERS

Some features of the phase diagram of SU(N) antiferromagnets on a square lattice, N. Read and S. Sachdev, Nuclear Physics B 316, 609 (1989).
Hole motion in a quantum Neel state, S. Sachdev, Physical Review B 39, 12232 (1989).
Valence bond and spin-Peierls ground states of low dimensional quantum antiferromagnets, N. Read and S. Sachdev, Physical Review Letters 62, 1694 (1989).
Sine-Gordon theory of the non-Neel phase of two-dimensional quantum antiferromagnets, W. Zheng and S. Sachdev, Physical Review B 40, 2704 (1989).
Spin-Peierls ground states of the quantum dimer model: a finite size study, S. Sachdev, Physical Review B 40, 5204 (1989).
Bond-operator representation of quantum spins: Mean field theory of frustrated quantum Heisenberg antiferromagnets, S. Sachdev and R.N. Bhatt, Physical Review B 41, 9323 (1990).
Action of hedgehog-instantons in the disordered phase of the 2+1 dimensional CP^N-1 model, G. Murthy and S. Sachdev, Nuclear Physics B 344, 557 (1990).
Spin-Peierls, valence bond solid, and Neel ground states of low dimensional quantum antiferromagnets, N. Read and S. Sachdev, Physical Review B 42, 4568 (1990).
Effective lattice models for two dimensional quantum antiferromagnets, S. Sachdev and R. Jalabert, Modern Physics Letters B 4, 1043 (1990).
Nature of the disordered phase of low dimensional quantum antiferromagnets, S. Sachdev, Electron Correlation and Disorder Effects in Metals, S.N. Behera ed., World Scientific, Singapore (1990).
Quantum antiferromagnets in two dimensions, S. Sachdev, Low dimensional quantum field theories for condensed matter physicists, Yu Lu, S. Lundqvist, and G. Morandi eds., World Scientific, Singapore (1995); cond-mat/9303014.
Finite temperature properties of quantum antiferromagnets in a uniform magnetic field in one and two dimensions, S. Sachdev, T. Senthil, and R. Shankar, Physical Review B 50, 258 (1994); cond-mat/9401040.
Spin-Peierls states of quantum antiferromagnets on the CaV₄O₉ lattice, S. Sachdev and N. Read, Physical Review Letters 77, 4800 (1996); cond-mat/9604134.
Translational symmetry breaking in two-dimensional antiferromagnets and superconductors, S. Sachdev and M. Vojta, Journal of the Physical Society of Japan 69, Suppl. B, 1 (2000); cond-mat/9910231.
Quantum criticality: competing ground states in low dimensions, S. Sachdev, Science 288, 475 (2000); cond-mat/0009456.
Quantum phases of the Shastry-Sutherland antiferromagnet, C.H. Chung, J.B. Marston, and S. Sachdev, Physical Review B 64, 134407 (2001); cond-mat/0102222.
Ground states of quantum antiferromagnets in two dimensions, S. Sachdev and K. Park, Annals of Physics (N.Y.) 298, 58 (2002); cond-mat/0108214.
Quantum phase transitions of correlated electrons in two dimensions, S. Sachdev, Lectures at the International Summer School on Fundamental Problems in Statistical Physics X, August-September 2001, Altenberg, Germany, Physica A 313, 252 (2002); cond-mat/0109419.
Bond and Neel order and fractionalization in easy-plane antiferromagnets in two dimensions, K. Park and S. Sachdev, Physical Review B 65, 220405 (2002); cond-mat/0112003.
Order and quantum phase transitions in the cuprate superconductors, S. Sachdev, Reviews of Modern Physics 75, 913 (2003); cond-mat/0211005.
Field theories of paramagnetic Mott insulators, S. Sachdev, Proceedings of the International Conference on Theoretical Physics, Paris, UNESCO, 22-27 July 2002, Annales Henri Poincare 4, 559 (2003); cond-mat/0304137.
`Deconfined' quantum critical points , T. Senthil, A. Vishwanath, L. Balents, S. Sachdev, and M. P. A. Fisher, Science 303, 1490 (2004); cond-mat/0311326.
The planar pyrochlore antiferromagnet: A large-N analysis, J.-S. Bernier, C.-H. Chung, Y. B. Kim, and S. Sachdev, Physical Review B 69, 214427 (2004); cond-mat/0310504.
Quantum criticality beyond the Landau-Ginzburg-Wilson paradigm, T. Senthil, L. Balents, S. Sachdev, A. Vishwanath, and M. P. A. Fisher, Physical Review B 70, 144407 (2004); cond-mat/0312617.
Quantum phases and phase transitions of Mott insulators , S. Sachdev in Quantum magnetism, U. Schollwock, J. Richter, D. J. J. Farnell and R. A. Bishop eds, Lecture Notes in Physics, Springer, Berlin (2004), cond-mat/0401041.
Deconfined criticality critically defined, T. Senthil, L. Balents, S. Sachdev, A. Vishwanath, and M. P. A. Fisher, Journal of the Physics Society of Japan 74 Suppl. 1 (2005); cond-mat/0404718.
Theory of Neel and valence-bond-solid phases on the kagome lattice of Zn-paratacamite, M. J. Lawler, L. Fritz, Y. B. Kim, and S. Sachdev, Physical Review Letters 100, 187201 (2008); arXiv:0709.4489.

NEXT ; PREVIOUS ; CATEGORIES