From Superfluid to Insulator: Bose-Einstein Condensate Undergoes a Quantum Phase Transition

Physics Today, volume 55, Number 3, page 18, March 2002

The atoms in a BEC assemble gregariously into a coherent whole, but in a periodic potential that's sufficiently strong, they can separate into an array of isolated atoms.

Bose-Einstein condensates (BECs) have opened yet another promising avenue of experimental research. This time, the road leads to an opportunity to study quantum phase transitions in a very clean and controlled manner. Specifically, researchers from the Max Planck Institute for Quantum Optics in Garching, Germany, and the University of Munich have shown that they can take a dilute gas of cold atoms from a superfluid to an insulator--and back again--simply by varying the intensity of a laser beam.¹ Daniel Kleppner of MIT said it was "breathtaking" to witness a quantum fluid move back and forth between its superfluid and insulating phases.

Matthew Fisher, a condensed matter theorist from the University of California, Santa Barbara, was excited to see BECs getting into the regime in which interactions between the bosonic atoms are driving qualitatively new effects. He is eager for experimenters to gain similar control over degenerate fermions as well. Aside from its intrinsic appeal, the capability demonstrated by the recent experiment might lead to such applications as controlled chemical reactions and quantum computation.

Phase transitions

Classical phase transitions are well known, the most obvious example being the melting of ice. At the melting point, thermal fluctuations drive the system from the liquid to the solid phase, or vice versa. A quantum phase transition is one that occurs at absolute zero: Thermal fluctuations are absent and the system is instead governed by quantum fluctuations.² Only in the past decade or two have theorists begun to study in earnest such quantum phase transitions, and it's been difficult to find experimental systems that bear close resemblance to the idealized models.

One example of a quantum phase transition is that between a superfluid and a Mott insulator. In a superfluid, the atoms move in phase with one another, all part of a single macroscopic wavefunction. In a Mott insulator, each atom occupies its own separate quantum well, unaffected by any of its neighbors. As different as these two phases are, they are described by the same Hamiltonian and are characterized by the competition between two interactions: the tendency of the particles to hop into adjacent wells, and the interparticle forces that keep them in separate wells. Depending on the relative strengths of these two interactions, the system can go from a superfluid to an insulator and back again, much as ice melts and refreezes as the air gets warmer or cooler.

A transition to a Mott insulator becomes possible when a superfluid like a BEC is placed in a periodic potential. In 1989, theorists used a Bose-Hubbard model, which describes interacting bosons in a periodic potential, to study transitions in a system like superfluid helium-4 absorbed in a porous medium.³ Their predictions could not be unambiguously validated because of the imprecisely known interactions and the presence of disorder, or imperfections, in the confining lattices.

Three years ago, a team of theorists from the University of Innsbruck in Austria and from Victoria University in New Zealand used the same model to analyze the phase transition of an ultracold, dilute gas of bosonic atoms placed in a periodic optical potential created by interfering pairs of laser beams.⁴ This team recognized that, with such a system, unlike in the porous ⁴He gels, experimenters had control over the relative strengths of competing interactions. Furthermore, disorder was unlikely to be present in such precisely made optical lattices.

The experiment

At the time of the Innsbruck-Victoria paper, experimenters were able to make optical lattices in one, two, and three dimensions, but they had not been successful in getting atoms to occupy more than a small percentage of the lattice sites. (To picture an optical lattice, think of the two-dimensional case, which is simply an egg-carton potential.) In 1998, Mark Kasevich and his group at Yale University loaded a BEC into an optical lattice to get many atoms in each well of a 1D lattice. For the recent experiment, the Munich group used the same approach in 3D. Participating in the experiment were Immanuel Bloch, Theodore Hänsch, Markus Greiner, Olaf Mandel, and Tilman Esslinger (now at ETH Zürich).

Bloch and company had to find room for the three pairs of lasers needed to create a 3D lattice, so they magnetically steered the ultracold atoms from a magneto-optic trap, which already has six lasers for cooling, to a separate trap (see the cover of this issue), where they formed a BEC and imposed the optical lattice.

With an average occupancy of one to three atoms per lattice site, the Munich group was able to vary the relative strength J of the tunneling between adjacent sites and the (repulsive) interaction energy U between two atoms. U is nearly fixed, but J gets weaker as the potential wells (whose heights are controlled by the laser intensities) get deeper. Think of the situation in 2D as one in which the potential is a landscape of peaks and valleys. In the superfluid phase, these undulations are small, and atoms move as a single coherent wavefunction, oblivious to the ripples below them. As the experimenters deepen the valleys by upping the intensity of the laser beams composing the lattice, the atoms at first remain in the coherent phase. But when the valleys become just a bit too deep, the atoms get localized in them, and the system enters the Mott insulating phase.

Figure 1

Interference patterns in absorption images (gauged by scale on right) result when a gas of cold atoms in a three-dimensional optical lattice is in its superfluid phase; no interference is seen in a Mott insulating phase. The depth of the potential wells in the lattice is systematically increased from 0 at (a) to 20 E_r at (h), where E_r is a reference energy. The phase transition occurs somewhere between (f) and (g). (Adapted from ref. 1.)

To find out what phase is present, the Munich researchers released the atoms from their trap and let them expand freely. They looked for the interference that's present when the atoms are in phase and absent when they are not. The interference pattern seen in panels a through f of figure 1 signals the superfluid phase. For the deeper wells shown in panels g and h, a Mott insulator has formed, as suggested by the disappearance of the interference pattern.

Amazingly, experimenters can take the atoms back and forth between these two phases. The phase coherence that's lost when the atoms enter the insulating state is promptly restored when the system re-enters the superfluid. The transition is rather sharp as a function of well depth and comes at a value that agrees with the predictions of the Innsbruck-Victoria group. Peter Zoller, an Innsbruck member of that team, said, "We are proud that our theoretical prediction was realized in the lab in an incredibly beautiful way."

Although the quantum phase transition technically occurs only at absolute zero, the atoms in the Munich experiment are sufficiently cold that the quantum fluctuations still dominate the thermal ones.

Number-squeezed states

A year ago, Kasevich, together with coworkers from Yale and the University of Tokyo had done a similar experiment, in one dimension: They formed a BEC, loaded it into a 1D optical lattice and saw the presence and absence of interference patterns as a function of well depth.⁵ The emphasis of their experiment was different, however, so that they had far more atoms--on the order of 1000--per lattice site. Kasevich and his coworkers are working on precision interferometry and want to have the large number of atoms to gain greater sensitivity.

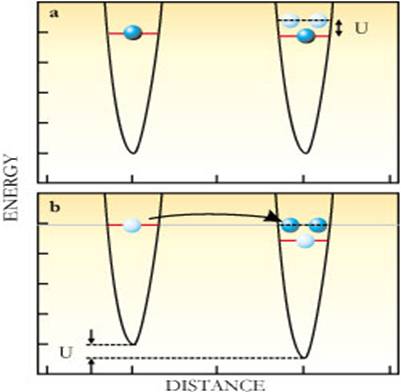
In both the Yale-Tokyo and the Munich experiments, the Mott insulating phase was in what is known as a number-squeezed state. That is, one could know with a very high degree of certainty how many atoms occupied each site. The price for such certainty, as dictated by the uncertainty principle, was that the phase was completely unknown. In the present case, the superfluid and Mott insulating phases are characterized by extreme cases of two conjugate parameters: In a superfluid, the phase is known but the number of atoms per site is undetermined, and in a Mott insulator the atom number is known but the phase is completely randomized.

Figure 2

(a) Two atoms (dark blue balls) occupy neighboring potential wells. U is the energy cost for them to be in the same well (pale blue balls). (b) Lowering one well relative to the other allows atoms originally in separate wells (light blue) to occupy the same well (dark blue). (Adapted from ref. 1.)

One prediction of the theory is that the formation of a Mott insulator should be accompanied by the opening of an energy gap in the excitation spectrum; as shown in the top panel of Figure 2, it costs an energy U to move an atom from the left-hand to the right-hand well. Bloch and his colleagues came up with a clever way to measure this energy gap. With the system in its insulating phase, they applied an energy gradient to the potential wells, which in 2D would be like tilting the egg carton. The effect is shown in the bottom panel of the figure: Once the energy gradient has raised the relative energy of the left-hand well by an amount U, the left-hand atom can hop, and both atoms end up on the same site. The tilt threshold that results in such tunneling tells experimenters the value of the energy gap U.

As for applications, Zoller said that the Mott insulator should allow interesting chemistry to happen. For example, "One might load exactly two atoms per lattice site and engineer the formation of molecules by way of a photoassociation process." Zoller and Ignacio Cirac (Max Planck Institute for Quantum Optics) have also proposed a scheme to entangle atoms for quantum computation using cold, controlled collisions.^6,7 Zoller views the Mott insulator as an ideal starting point for their scheme.

Barbara Goss Levi

References

1. M. Greiner, O. Mandel, T. Esslinger, T. W. Hänsch, I. Bloch, Nature 415, 39 (2002).

2. S. Sachdev, Quantum Phase Transitions, Cambridge U. Press, New York (2001).

3. M. P. A. Fisher, P. B. Weichman, G. Grinstein, D. S. Fisher, Phys. Rev. B 40, 546 (1989).

4. D. Jaksch, C. Bruder, J. I. Cirac, C. W. Gardiner, P. Zoller, Phys. Rev. Lett. 81, 3108 (1998).

5. C. Orzel, A. K. Tuchman, M. L. Fenselau, M. Yasuda, M. A. Kasevich, Science 291, 2386 (2001).

6. D. Jaksch, H.-J. Briegel, J. I. Cirac, C. W. Gardiner, P. Zoller, Phys. Rev. Lett. 82, 1975 (1999).

7. D. Jaksch, J. I. Cirac, P. Zoller, S. L. Rolston, R. Cote, M. D. Lukin, Phys. Rev. Lett. 85, 2208 (2000).