Experiments Vindicate a 50-Year-Old Explanation of How Liquid Metals Resist Solidification

Physics Today, volume 56, Number 7, page 24, July 2003

Diffracted x rays reveal a sequence of structural changes in a levitated drop of metal as it cools and freezes.

A metal's density barely falls on melting. One might guess, therefore, that metal atoms in the liquid phase pack together with almost the same efficiency and with almost the same order as in the solid phase. And--to continue this line of speculation--if one tried to cool a liquid metal below its equilibrium melting point, the few disorderly atoms would easily fall into line with the ordered majority and the liquid would promptly solidify.

In fact, as David Turnbull and Robert Cech showed in 1950, liquid metals can be cooled tens to hundreds of degrees below their equilibrium melting temperatures without solidifying.¹ The trick is to prevent any impurities or other extraneous components from nucleating the nascent solid.

According to classical nucleation theory, a liquid solidifies when thermal fluctuations push it over an energy barrier. This nucleation barrier, W, depends on ΔG, the difference between the free energy of the liquid and solid phases. Specifically, W ~ ΔG^-2. As a liquid cools, ΔG increases and lowers the nucleation barrier.

But classical theory also has W proportional to γ³, where γ is the energy of the interface between the liquid and solid phases. Turnbull and Cech could undercool their samples because, for metals, the interfacial energy is far higher than one might expect based on density alone.

In 1952, to account for the unexpectedly large γ, Charles Frank put forward a now classic hypothesis.² It's possible to undercool metals, he argued, because of a fundamental mismatch in the way atoms arrange themselves in the liquid and solid phases.

According to Frank, atoms in the liquid possess a short-range order based on the icosahedron. One of Plato's perfect solids, the icosahedron has 20 triangular faces.

Frank picked icosahedral order because it's among the tightest and least energetic ways to arrange a small number of atoms. But because of their fivefold symmetry, icosahedral clusters can't combine to form a regular crystal. Frank saw that the energy cost of creating an interface between such structurally incompatible phases would be high.

When Frank published his paper, he didn't know about quasicrystals, some of which possess icosahedral order. But if he had known about them, he might have proposed the following test of his hypothesis:

Identify a material that has both a metastable quasicrystalline phase and a stable crystalline phase. Melt the material and let it cool. The falling temperature lowers the nucleation barriers of both the quasicrystalline and crystalline phases. But because the liquid and quasicrystal phases have similar order--and hence a smaller γ--the quasicrystalline phase has the lower barrier and will solidify first. Eventually, the temperature drops to the point that the second barrier is low enough for the metastable phase to hop over and form the crystal.

Ken Kelton of Washington University in St. Louis, Missouri, didn't set out to perform this hypothetical task, but that's what he and his collaborators ended up doing. Their project, which involved levitating drops and using a state-of-the art synchrotron, not only proves Frank's hypothesis, but also challenges theories of how crystals form.³

Electrostatic levitation

Undercooling liquid metals is difficult. Even if a sample is free from impurities, any bump or crevice on the walls of the vessel that contains it can nucleate the solid phase at the equilibrium melting temperature.

Turnbull and Cech addressed the container problem by melting samples on flakes of amorphous silica. They assumed that the amorphous substrate would be a poor nucleator of crystalline structure. But ideally, one dispenses with a container. Thanks to surface tension, a drop of molten metal holds itself together. So, to achieve the containerless ideal, one levitates the drop and, for tracking structural changes, keeps it motionless in a beam of x rays or neutrons.

Figure 1

Schematic diagram of the electrostatic levitation chamber installed in an x-ray beamline. (Courtesy of Ken Kelton.)

Several levitation methods exist. Kelton opted for electrostatic levitation and, for help, turned to Jan Rogers of NASA's Marshall Space Flight Center in Huntsville, Alabama. Rogers and her coworkers Bob Hyers, Tom Rathz, and Mike Robinson developed the levitation chamber that appears on this month's cover and schematically in figure 1.

Before electrostatic levitation can begin, the initially solid drop is charged by induction. Electrodes above and below the drop create the levitation field, which, being electrostatic, lacks minima. Keeping the drop in place, therefore, is like balancing an upended broom: It requires an active feedback system. The Marshall feedback system uses cameras and computer control. With it, the 2-mm-sized drop can be held steady with a precision of 50 μm.

A laser melts the drop, which cools radiatively. The drop's thermal radiation spectrum provides the temperature diagnostic.

Recalescence

Kelton's original plan was to study titanium-zirconium-nickel. The alloy forms metastable icosahedral quasicrystals, but Kelton was focusing instead on the alloy's stable crystalline phase, a complex polytetrahedral arrangement called C14 Laves.

Figure 2

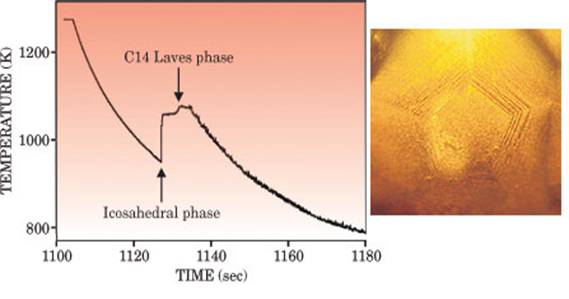
As a molten drop cools, its temperature rises sharply at two specific phase transitions (left). First, when the liquid forms the metastable icosahedral phase, which is quasicrystalline, and later when it forms the C14 Laves phase, which is crystalline. An optical mircograph (right) of the 2-mm-sized drop in its metastable state reveals pentagonal ridges. (Courtesy of Ken Kelton.)

In preliminary levitation experiments at Marshall, Kelton and his Washington University colleagues Geun Woo Lee and Anup Gangopadhyay measured the temperature of a cooling drop of Ti-Zr-Ni. As figure 2 shows, the drop's steady decline in temperature is interrupted twice by two abrupt jumps. The jumps, termed recalescences, correspond to the release of latent heat at a phase transition.

Kelton suspected that the first recalescence signaled the formation of the alloy's metastable icosahedral phase, followed five seconds later by the formation of the C14 Laves phase. Viewing the metastable phase through an optical microscope confirmed its fivefold symmetry (figure 2). Here, Kelton realized, was a likely material for testing Frank's hypothesis.

Confirming Frank's hypothesis involves not only undercooling the right material, but also measuring its atomic structure. And that involved a trip to the Advanced Photon Source at Argonne National Laboratory in Illinois. At the APS, Doug Robinson and Alan Goldman helped Kelton and his team to position the electrostatic levitation chamber in one of the synchrotron's beam lines.

A so-called third-generation synchrotron source, APS produces x rays of high brightness and high energy. Both qualities were invaluable for Kelton's experiment: The brightness made it possible to collect data with high signal-to-noise on the few-second timescale of the solidification, while the energies (125 keV, λ = 0.99 Å) made it possible to do a transmission experiment rather than a more difficult reflection experiment.

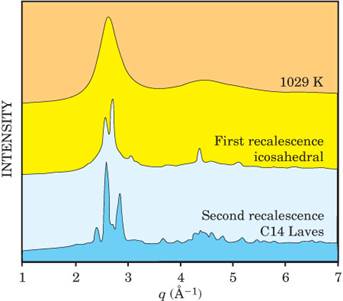
figure 3 shows three representative diffraction patterns taken at different stages after the laser had melted the drop. The peaks appeared in the right places for both the solid icosahedral and C14 Laves phases. Frank was vindicated.

Nucleation theory

Figure 3

X-ray diffraction patterns capture the structural changes as the molten alloy (top) cools to solidify first into the icosahedral phase (middle) and then to the C14 Laves phase (bottom). The peaks occur at the predicted locations and are plotted as a function of the momentum transfer q = 4π sinθ/λ, where θ is the scattering angle and λ is the x-ray wavelength. (Adapted from ref. 2.)

Figure 3 captures snapshots of the two solid phases, but Kelton and his colleagues could also obtain diffraction patterns at various points along the cooling curve. That's especially interesting for comparing experiment with theories of how crystals form.

Diffraction patterns depend on experimental setup. To compare experiment with theory, one calculates structure factors S(q), where q is the momentum transfer. Constructing S(q) from data involves modeling various aspects of the experiment, such as the transmission of the levitation chamber's beryllium windows. Constructing S(q) from theory involves choosing an interatomic potential then doing either a large-scale computer simulation or an approximate theoretical analysis.

In the early 1980s, before the discovery of quasicrystals, Frank's ideas about local icosahedral ordering were applied to the formation of metallic glasses. Harvard University's David Nelson and his graduate student Subir Sachdev calculated temperature-dependent structure factors for glass-forming liquids.⁴ At large values of q, which probe short-range order, their S(q) exhibits a pair of peaks and a shoulder that grows as the temperature drops. Kelton found the same features and the same temperature dependence in the S(q) he derived from his data.

The existence of icosahedral order in the solidifying liquid has implications for classical nucleation theory. In that picture, nucleation starts, or fails to start, in small volumes. When the volume occupied by the nucleating phase exceeds the so-called critical volume, fluctuations favor the formation of the new phase.

From his data, Kelton derived both the size of the icosahedral clusters in the liquid and the critical volume. Both turned out to be a few nanometers across. The similarity of the two scales suggests that a liquid metal isn't a structural blank slate. Structural correlations in the liquid could affect crystallization.

The small scale of the critical volume reveals a limitation of classical theory. When the crystallizing action takes place on the scale of a few tens of atoms, it's unlikely that a clear-cut, classical interface is appropriate. The challenge is to make nucleation theory more atomistic.

Other levitations, other systems

That a single system, Ti-Zr-Ni, was observed to form a quasicrystalline phase and then a crystalline phase was the key to proving Frank's hypothesis. But the 50-year-old theory had received impressive support from similar work done by other groups.

The first to study the structure of levitated drops were Dirk Holland-Moritz of the German Aerospace Research Establishment (DLR) in Cologne and his collaborators. The DLR team used electromagnetic levitation, which exploits an EM field to provide both levitation, through Lenz's law, and heating, through surface eddy currents.

Ten years ago, the DLR team showed that systems that have a high degree of icosahedral order in the solid phase can be undercooled further than systems that lack or have less icosahedral order.⁵

And last year, the DLR team and their collaborators from two French institutions--Paris-Sud University and the Center for Nuclear Studies in Grenoble--demonstrated for four elemental metals and three alloys that the further a liquid undercools, the greater its icosahedral order.⁶

Charles Day

References

1. D. Turnbull, R. E. Cech, J. Appl. Phys. 21, 804 (1950).

2. F. C. Frank, Proc. R. Soc. London, Ser. A 215, 43 (1952).

3. K. F. Kelton et al., Phys. Rev. Lett. 90, 195504 (2003).

4. S. Sachdev, D. R. Nelson, Phys. Rev. Lett. 53, 1947 (1984) .

5. D. Holland-Moritz, D. M. Herlach, K. Urban, Phys. Rev. Lett. 71, 1196 (1993) .

6. T. Schenk et al., Phys. Rev. Lett. 89, 075507 (2002) .